Filter for the arctangent function to remove discontinuities
While taking a course in robotics mechanics, I needed a way to remove discontinuities from the arctangent function. The arctangent function can be defined in two ways:
- Single-input parameter: The output range spans from -π/2 to +π/2.
- Two-input parameter (atan2): The output range spans from -π to +π, effectively doubling the range.
While this works well for many applications, it introduces discontinuities when dealing with angles that exceed ±π. For example, consider a continuously increasing angle:
- The angle starts at 0, increases to π, and then exceeds π.
- However, the inverse tangent of this angle will not produce a smooth output. Instead, it will jump from +π to -π at the discontinuity, creating a sawtooth-like pattern.
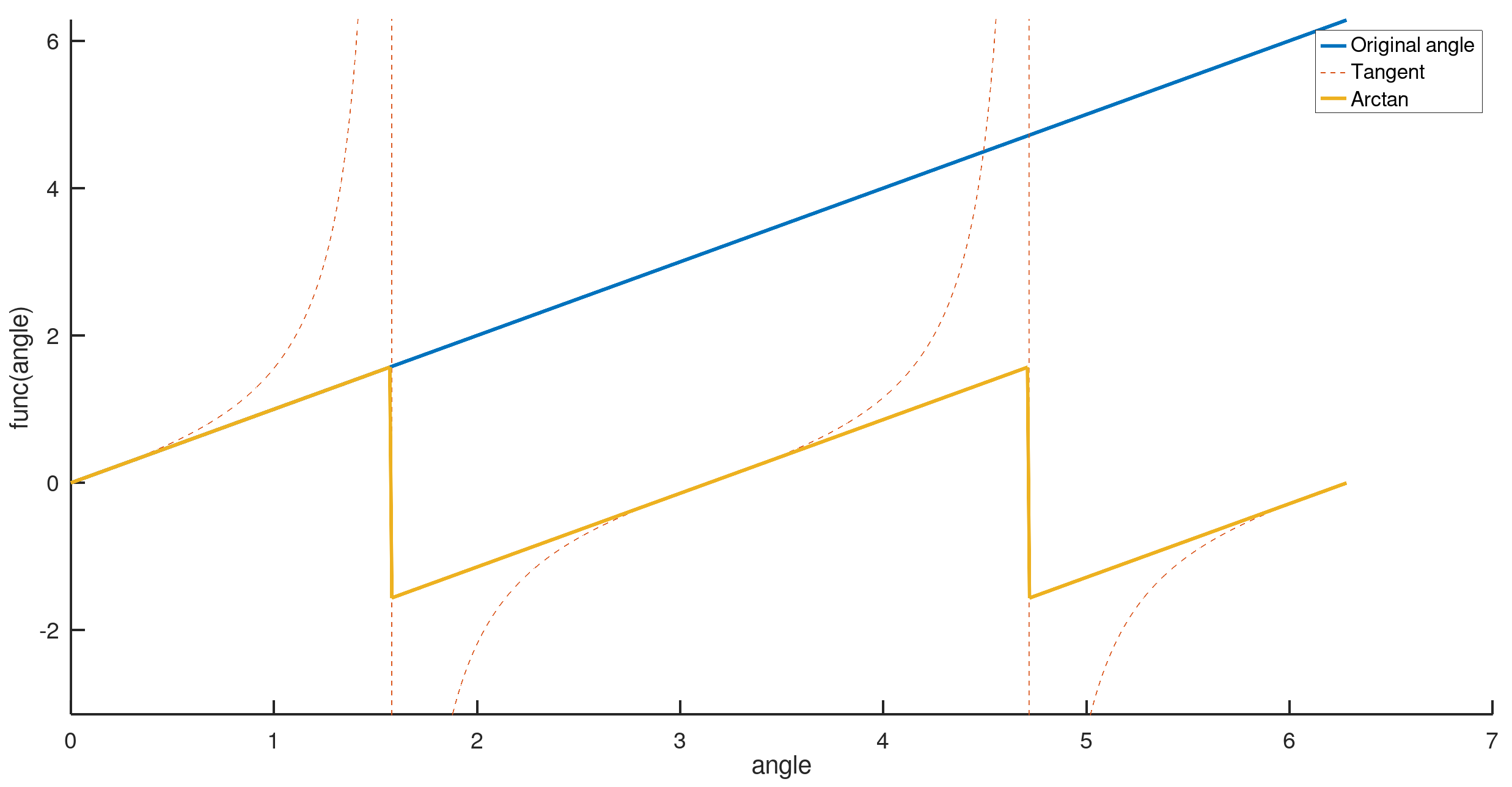
If the angle is only used for geometric orientation (e.g., aligning a surface or body), the discontinuity is irrelevant as any orientation can be represented within ±π. However, if we need to compute time derivatives or integrals of the angle, the discontinuities cause major issues:
- For a smoothly changing angle, the derivative should be constant.
- But with jumps at ±π, the derivative will have abrupt spikes at each discontinuity.
To address this, I developed a filter that removes discontinuities by:
- Using the derivative of the original (discontinuous) angle to predict the next value.
- Detecting when a sample crosses the ±π boundary.
- Applying an offset (±2π) to eliminate the jump.
Here’s the implementation in Octave/MATLAB:
function [filter] = continuityFilter(angles)
%% Filter to remove discontinuity of atan2() function near angle = +-PI
% This process ensures the numerical derivatives of said angle are continuous
% axis lengths
len_y = length( angles(:,1) );
len_x = length( angles(1,:) );
% copy inputs
filter = angles;
% scan axes
for y = 1:len_y
offset = 0;
for x = 3:len_x % x >=3
% estimate current value via past slope
angle_now = angles(y, x);
angle_last = angles(y, x-1);
angle_last2 = angles(y, x-2);
angle_expected = 2*angle_last - angle_last2;
% accumulate rotations
if (angle_expected < -pi) && (angle_now > 0)
offset = offset - 2*pi;
elseif (angle_expected > pi) && (angle_now < 0)
offset = offset + 2*pi;
end
% offset input values
filter(y, x) = filter(y, x) + offset;
end
end
end
This filter works well for smooth, continuous angle changes. However:
- It relies on finite differences to estimate derivatives.
- If the data points are too far apart, the derivative approximation fails, and the filter may not correct discontinuities properly.
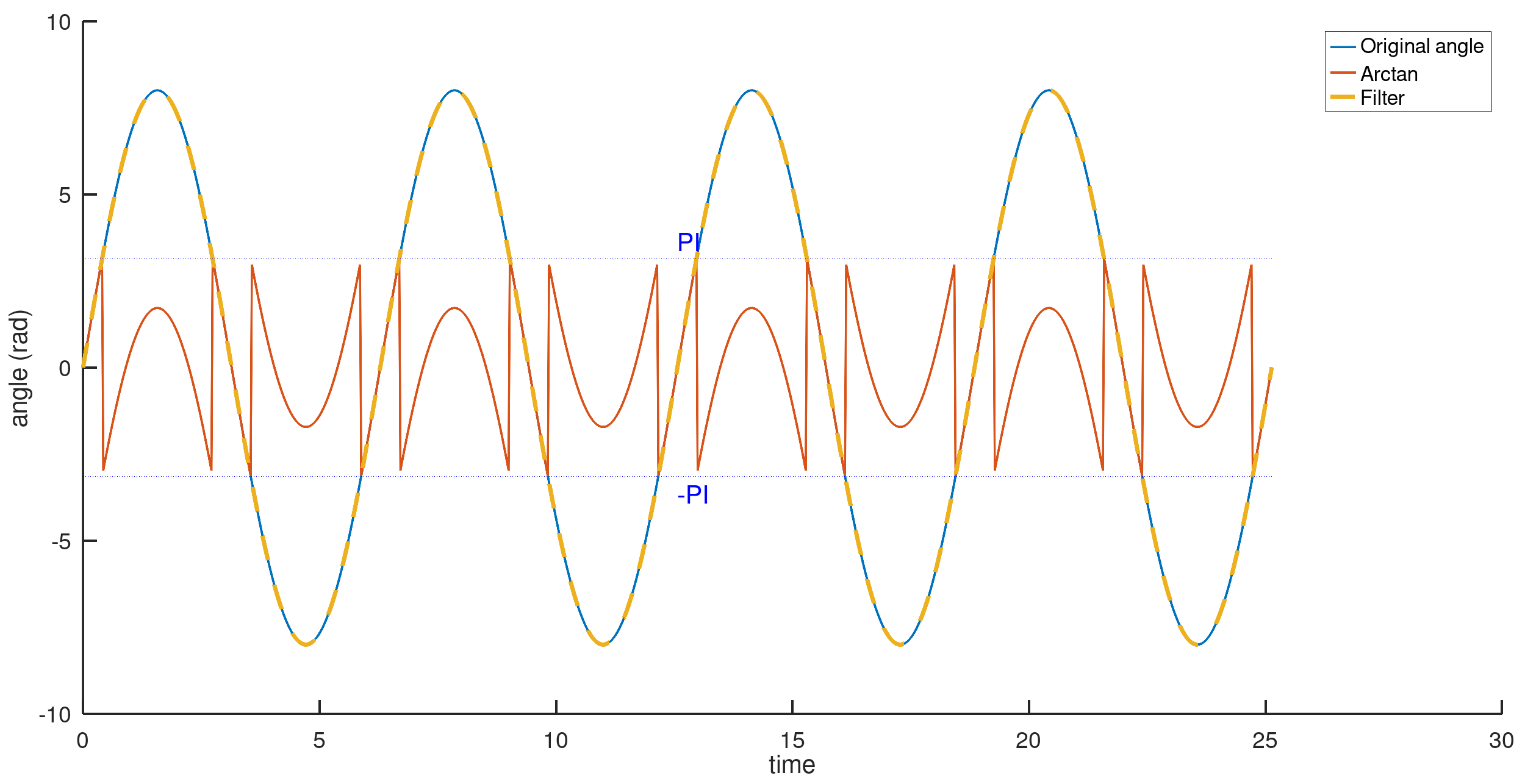
The plot below shows:
- An angle defined as a high angle sine wave.
- The discontinuous output of
atan2(sinθ, cosθ). - The filtered output, which matches the original sine wave/angle.
Code
All octave scripts used for this post are available below: