Datatypes for 3D vectors and quaternions
While developing an algorithm to perform sensor fusion between the gyroscope and accelerometer of an inertial measurement unit, I needed a way to execute basic vector operations and manipulate a quaternion to encode the gyroscope’s heading. Although it was possible to hard-code these operations directly into the sensor fusion, it seemed prudent to separate this functionality in case it needed to be reused. This was especially relevant for spatial navigation, which requires manipulating vectors in different frames of reference.
To create data types for vectors and quaternions, I first needed to understand the operations they can perform. These operations, defined through mathematical notation, had to be converted into functions. By using operator overloading, I was able to employ these functions in a way that closely resembled mathematical notation. This is because an operation is simply a different way of writing a function that takes one or more parameters. This approach was applied to most of the operations possible for vectors and quaternions. For more information on vector and quaternion operations, see these links:
For example, the addition of two vectors can be written as V1 + V2. The + sign serves as shorthand for the function that takes two vectors and returns a new vector of their added values. When it came time to actually use these data types in code, it was straightforward because the corresponding operations could be written just as they would be in mathematical notation. This simplicity made the code easier to read, as operations reduced to a symbol rather than a function call.
Inside the library, vectors and quaternions were declared as structs to define their data types. Both vectors and quaternions could perform basic operations such as addition, subtraction, multiplication, division, increment, decrement, and their analogs for multiplication and division. Vectors and quaternions were also compatible with each other through operations such as the vector dot product and cross product. Quaternions could be constructed as unit quaternions to represent rotations, allowing them to be directly used to rotate vectors. Additionally, both data types were made compatible with arrays, meaning that a length-3 array could be added, subtracted, etc, from a vector. This compatibility also extended to quaternions.
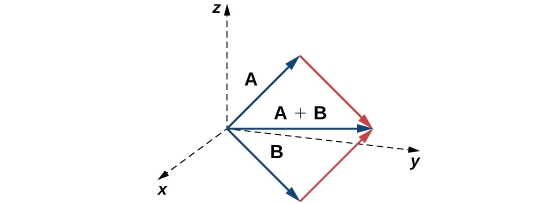
3D Vectors represent magnitude and direction
Vectors were the first data type to be defined as they were the more primitive structure. They consisted of an array with three components that could be manipulated to perform basic operations. Quaternions inherited from vectors by adding an additional scalar component to their structure. These four values, due to the mathematics of quaternions, allowed them to encode the rotations of vectors in three-dimensional space, enabling the quaternion data structure to act upon vectors through specific functions.
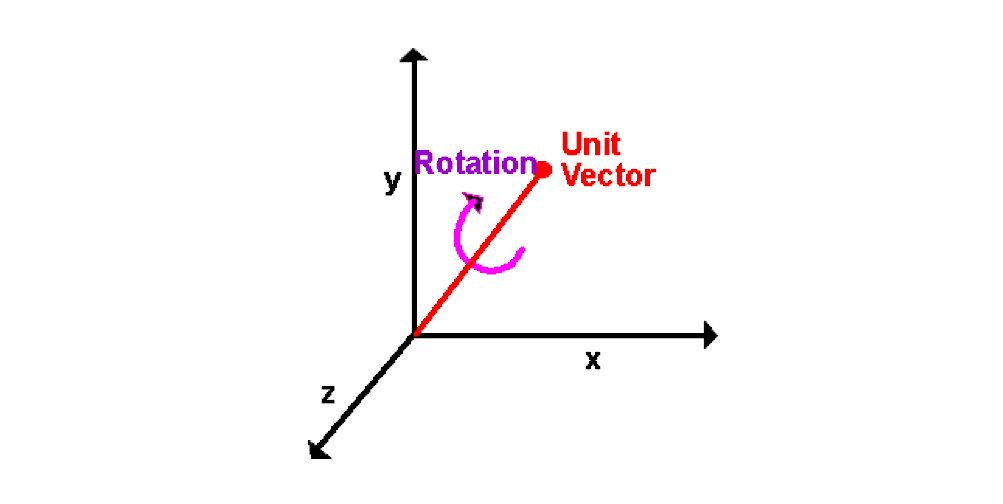
4D Quaternions represent an axis of rotation and rotation angle
Overall, I was very pleased with this project. I found it enriching because it taught me to view operations as functions and to see algebraic representations as translatable into code. It also helped me understand that what we do on paper is merely a representation of operations that are procedural, following an input-output pattern. All the intermediate steps we perform are just a way to keep track of these operations. This step-driven nature emphasizes that these operations are algorithmic, in that they following a precise series of steps to achieve an output. I feel this experience increased my mathematical maturity by providing a more nuanced perspective on math.
GitHub Repository
The library can be downloaded from its GitHub repository or the Arduino library catalog. See the following link to access the repository: VectorDatatype