Algorithm comparison

During college, I took a course in data structures based on C++. This was a standard course required for anyone interested in computer science. As part of the final grade, I had to submit a report comparing different sorting algorithms. I analyzed their effectiveness and the time taken for each to complete its operations. This comparison was meaningful because different algorithms converge towards a specific time complexity when dealing with large datasets.

For example, an algorithm’s execution time can increase linearly with the size of the dataset; if you double the dataset, it takes twice as long for the algorithm to complete. Alternatively, an algorithm can increase logarithmically with the dataset, meaning a significant increase in the amount of information has a relatively minor effect on the processing time. This is ideal, as the algorithm can handle more data without a substantial slowdown. Conversely, some algorithms exhibit quadratic behavior; if you double the sample size, the execution time increases fourfold. This is problematic, as even minor increases in data can significantly extend processing time. Analyzing these algorithms allows us to predict their execution times, which is crucial in time-critical situations where optimal performance is desired.

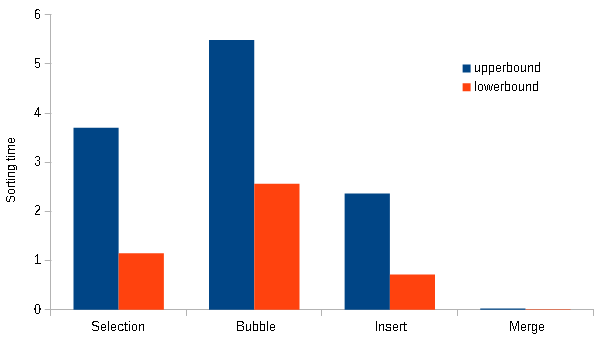
In this empirical study, four different sorting algorithms were compared: Selection sort, Bubble sort, Insertion sort, and Merge sort. Each algorithm was tasked with sorting an array filled with random integer values. The array contained 15,000 entries, and the random values ranged from 0 to 1000. To ensure consistent results, a single random array was generated for each algorithm to sort, and the execution time of each was recorded.

This approach allowed for a fair comparison, as all algorithms sorted the same array. Any differences in execution time could then be attributed to the algorithms themselves rather than to variations in the input arrays. Once the initial testing sequence was complete, the entire process was repeated with a newly generated random array, and this was done 20 times. The results of the twenty separate tests revealed a clear trend when average times were analyzed:

Overall, Merge sort was the fastest of all the algorithms, with an average execution time an order of magnitude lower than the others. This superior performance is likely due to its efficiency in avoiding unnecessary comparisons.
Bubble sort was the slowest algorithm, taking nearly twice as long as the next slowest. It only compares adjacent entries, which limits its ability to identify more distant entries that could be compared and swapped. As a result, it performs many unnecessary swaps with minimal sorting effect.
Selection sort was the second slowest algorithm. Although it does not perform as many trivial swaps as Bubble sort, it often leaves the array mostly unchanged after a swap, leading to more scans, swaps, and extended execution time.
Insertion sort was the second fastest algorithm. While not as quick as Merge sort, it significantly outperformed the other algorithms. This can be attributed to its method of displacing each entry that it scans, which reduces unnecessary comparisons by biasing larger values towards one side of the array.

In terms of variation between executions of the same algorithm, a different trend emerged:

Merge sort had a much lower standard deviation than the other algorithms, indicating that its execution time varied little with input arrays. The extent to which the random array was ordered had minimal effect; there was neither a “favorable” nor “unfavorable” input.
Bubble sort exhibited the largest standard deviation. The level of “sortedness” in the input array significantly affected its execution time.
Selection sort and Insertion sort showed similar standard deviations. Between the two, Insertion sort was slightly more sensitive to the order of the input array, but not by much. In either case, the “sorting” of the input had a notable impact on execution time.

Although Merge sort was the fastest and most consistent algorithm, the overhead required to excute it may be a drawback. If the input array is partially sorted, it may be possible to use a simpler sorting algorithm that completes the operation in an acceptable ammout of time. If low overhead is important, then the slower algorithms may possess qualities worth using.

Linked-list data structure

For another assignment, I had to implement a data structure known as a linked list. This interconnected structure stores data in a way that resembles a chain, where individual elements are linked to one another, and each element can hold a specific amount of information. This data structure is flexible and allows different elements to be inserted at various positions along the linked list. However, there must always be an element at the head of the list and an element at the end.

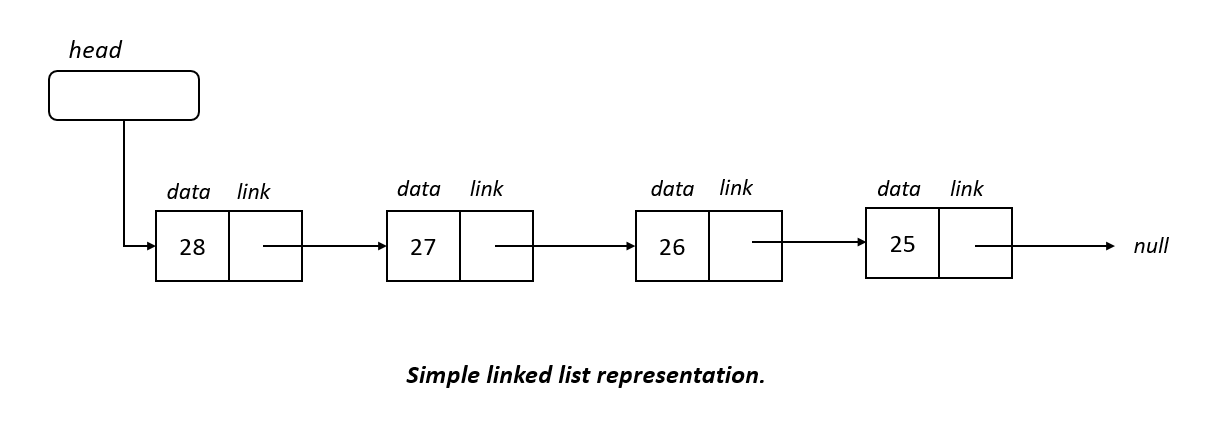
This structure permits an arbitrary number of elements to be added to the list. Similarly, we can remove elements until no items remain. This flexibility distinguishes linked lists from other data structures like arrays. In an array, the number of elements is predetermined. While we can replace the data stored in each element, we cannot always delete elements or add more to increase its length. The behavior of these data structures, however, can vary depending on the programming language in use.

In some languages, the length of an array can be modified after its creation, allowing it to mimic the behavior of a linked list more closely. In the case of C++, we can easily declare arrays with an initial length. However, modifying the length or adding entries to the array afterward can be more complicated. Therefore, creating a linked list data structure may be advantageous depending on the data being stored. For instance, we might want to create a linked list that stores classes, which can contain more complex information. In this case, a linked list helps maintain a known relationship between each element, enabling the development of a more sophisticated program.

Github repository

SortingAlgorithmCompare